Раскрой материала

На раскрой поступают заготовки определенного материала (металлический прокат, листы стекла, фанеры, ткани, шкуры, резины и т. д.) стандартного размера, с которого производят изделия разного вида: детали одежды или обуви, элементы строительных конструкций, мебелей и так далее. Существуют несколько способов раскроя заготовки, при помощи которых можно производить определенное количество изделий определенных видов, для каждого с которых известны отходы материала. Необходимо выполнить заказ на производство заданного количества изделий определенного вида таким образом, чтобы минимизировать общие отходы.
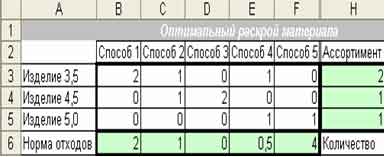
В нашем случае, из заготовки ограниченного количества (103 шт.) длиной 9 м нужно раскроем сделать изделия 3 видов длиной 3,5 м, 4,5 м и 5 м. Возможны 5 способов раскроя материала с соответствующими нормами отходов. Дополнительное условие: количество изделий должно отвечать ассортименту 2:1:1. Определить оптимальный план раскроя (каким способом и сколько заготовок раскроить), чтобы общие отходы были минимальны.
Экономико-математическая модель.

Найти план раскроя, при котором
Общие отходы - min
При ограничениях: Сума(общие количество раскроенных заготовок) = Количество заготовок; 2*Изделие_3,5=1*Изделие_4,5=1*Изделие_5 и при граничных условиях: все неизвестные больше нуля и целые числа.

Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Об_отходы):

столбец Всего заполняем формулами: =СУММПРОИЗВ(Изделие_способ;План);
столбец Ограничение заполняем формулами: Ассортимент*Всего;
в ячейку Сума вводим формулу сумы по строке Плана;
строку Отходы заполняем формулами: План*Норма_отходов;
в целевую ячейку Об_отходы вводим формулу суммы по строке Отходы.

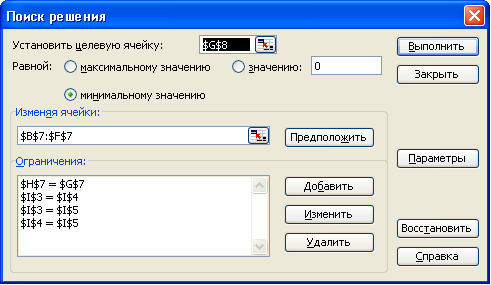
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.

Анализ результатов.
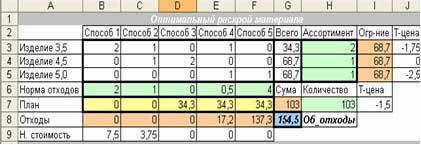
Чтобы отходы были минимальными (154,5) нужно раскроить по 34,3 заготовок 3, 4 и 5 способами. Теневые цены ограничений на ассортимент показывают на сколько уменьшиться целевая ячейка, если мы увеличим количество соответствующего изделия на 1 ед. Теневая цена на количество заготовок показывает на сколько уменьшаться общие отходы при увеличении числа заготовок на 1 ед.
Нормированные стоимости плана показывают как увеличатся общие затраты если мы принудительно будем использовать «невыгодный» способ для 1 ед. количества заготовок.

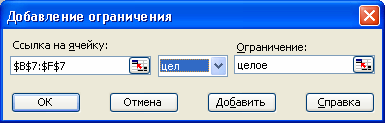
После анализа добавляем ограничения: План – целые числа.

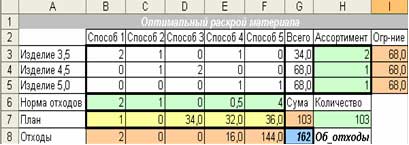
Теперь видим, что «выгодными» стали четыре способа раскроя: 1, 3, 4 и 5, при которых общие отходы равны 162. Увеличение общих отходов объективно связаны с неделимостью значений неизвестных.